L’analyse quantitative des risques réalisée dans un projet permet d’associer à chaque risque une probabilité d’occurrence et un impact, décrit par une variable aléatoire. Ces risques doivent alors être regroupés pour définir le risque global associé au projet. Ce risque global est obtenue en faisant la somme de tous les risques élémentaires.
- Un exemple simple: le tirage de 2 dés
- Simulation de Monte-Carlo
- Les résultats
- Exemple
- Intérêt
- Application disponible en ligne
1 – Un exemple simple: le tirage de 2 dés
Un dés possède 6 faces, numérotés de 1 à 6. Si le dés n’est pas truqué, toutes les faces sont équiprobables avec une probabilité de 1/6. Le tirage d’un dés est donc représenté par une variable aléatoire Uniforme discrète dont les valeurs vont de 1 à 6 avec une probabilité de 1/6.
Lorsque l’on tire 2 dés, la somme est comprise dans l’intervalle [2; 12 ], 2 quand on obtient (1,1) et 12 avec (6,6). Quelles sont les probabilités associées. Pour les calculer on peut procéder au dénombrement de l’ensemble des résultats.
Le tableau suivant affiche pour chaque résultat l’ensemble des paires permettant de l’obtenir. Il y a par exemple 6 paires permettant d’obtenir la valeur 7. Le nombre total de paires étant égal à 36, la probabilité de 7 est égale à 6/36 soit 1/6 soit 0,16666…7 arrondie ici à 0,167.
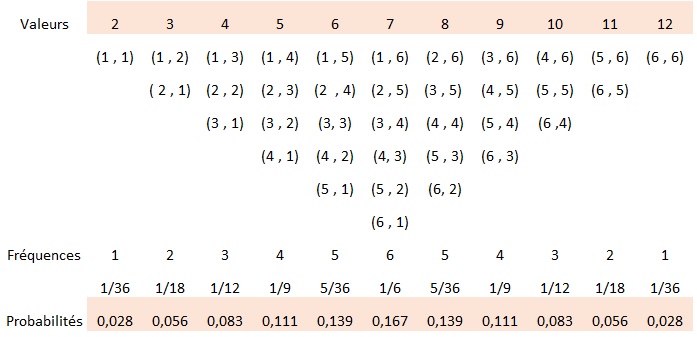
Calcul des probabilités par dénombrement des résultats possibles.
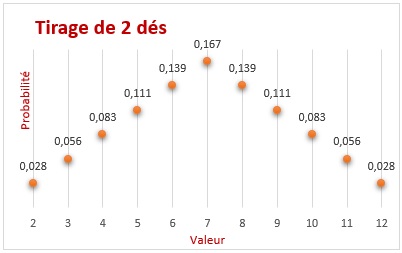
Représentation graphique de la loi de probabilité du tirage de 2 dés
Le résultat du tirage de 2 dés est donc une variable aléatoire (VA) discrète définie par les couples (x, px) où x prend les valeurs 2 à 12 et px les probabilités associées. Le graphique de droite représente la distribution de probabilité de cette VA.
Remarque 1 – Si vous jouez à ce tirage avec des amis, vous avez intérêt à parier sur 7 et les valeurs qui en sont proches (pour ne pas trop attirer l’attention).
Remarque 2 – La somme de 2 VA de loi Uniforme est une VA de loi Triangulaire (Cf. graphique ci-dessus).
Remarque 3 – Vous pouvez calculer les probabilités sans passer par le dénombrement exhaustif présenté ci-dessus. Il suffit de faire plusieurs tirages consécutifs des 2 dés, en incrémentant chaque fois d’une unité la colonne de la valeur obtenue. Après « suffisamment » de tirages, la probabilité de chaque valeur s’obtient en divisant la fréquence de chaque valeur par le nombre total de tirages. Cependant, comme la précision du résultat s’améliore avec le nombre de tirages, il faut en faire « un certain nombre » pour avoir une estimation « acceptable ».
Remarque 4 – Le « certain nombre » mentionné ci-dessus dépend du nombre et de la nature des VA à additionner. Faites l’expérience avec 2 dés pour voir à partir de combien de tirages vous obtenez des probabilités suffisamment proches des valeurs théoriques affichées dans le tableau. Selon le cas, ce nombre se définit en centaines, en milliers, en dizaines de milliers, etc. Il est alors nécessaire de remplacer les tirages manuels par des algorithmes informatiques.
2- Simulation de Monte-Carlo
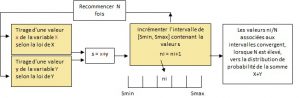
La somme de variables aléatoires (VA) est obtenue par simulation de Monte-Carlo. Cette technique est décrite par le schéma suivant qui effectue la somme des 2 variables aléatoires X et Y (S = X + Y), X étant compris entre Xmin et Xmax et Y entre Ymin et Ymax.
A chaque itération, on tire une valeur x (resp. y) dans la loi de la VA X (resp. Y), puis on fait la somme des deux valeurs.
- N est généralement compris entre 5000 et 100 000 ;
- Smin = Xmin + Ymin et Smax = Xmax + Ymax
- La somme des deux VA est incluse dans l’intervalle [Smin; Smax] que l’on découpe en Nc intervalles pour définir un histogramme de Nc classes;
- A chaque itération (ou tour), on obtient une valeur x (resp. y) de X par tirage aléatoire dans la distribution de X (resp. Y). Ces tirages donnent des valeurs différentes à chaque itération;
- La somme x+y se trouve dans une classe de l’histogramme. Le nombre ni de réalisations dans cette classe est incrémenté d’une unité : ni = ni + 1
- Lorsque le nombre d’itérations est suffisamment élevé, le rapport ni/N est égal à la proportion pi de valeurs de S dans la classe i;
- Ces pi, associés par exemple à chaque centre de classe, définissent la distribution de probabilité de la variable aléatoire S. Il est ainsi possible de donner une représentation graphique de cette variable;
- Les paramètres de la variable S (la moyenne, l’écart type, etc.) sont calculés pendant la simulation.
Remarque
Lorsque les risques ne sont pas indépendants, leur sommation doit tenir compte des liens éventuels. Une façon d’introduire ces liens consiste à définir des corrélations entre certaines variables. Les algorithmes de génération de nombres aléatoires doivent alors tenir compte de ces corrélations. Ignorer les dépendances entre les variables a pour effet de réduire l’écart type de la somme et donc de sous-estimer le risque global. Cette approche engendre deux difficultés : d’une part définir les corrélations croisées entre les risques (qui peuvent se compter en centaines) et d’autre part générer des valeurs aléatoires qui tiennent compte de ces corrélations. Afin d’éviter ces difficultés, tout en ne dégradant pas trop les résultats, il est nécessaire de définir les risques de telle sorte qu’ils soient indépendants. La meilleur façon de procéder consiste à regrouper les risques qui présentent des dépendances notables en un seul risque.
3 – Les résultats
Les risques étant des variables aléatoires, leur somme S est une variable aléatoire qui représente le coût du risque global. Elle est définie par les résultats suivants.
- L’histogramme de la distribution de probabilité de S qui permet de tracer la courbe représentative de cette distribution;
- Les valeurs min et max;
- La moyenne;
- L’écart type qui mesure la dispersion autour de la moyenne;
- Le quantile à 90% est égal à la valeur de S qui n’est dépassée que dans 10% des cas. Cette valeur, qui représente le Max de S avec un risque de 10% d’être dépassé est appelée « Valeur à Risque (VaR) ». Autre formulation: 90% des valeurs de S sont inférieures à VaR90.
La provision pour risque d’un projet est généralement définie par un quantile associé à une probabilité de couvrir le risque: VaR80, VaR85, Var95, etc.
4 – Exemple
Cet exemple simple est limité à un ensemble de risques projet dont on souhaite faire la somme afin d’estimer une provision pour risques. Il est construit avec les 15 risques fictifs nommés r1 à r15 qui sont décrits dans le tableau suivant.
| Risques | Probabilité d'occurrence | Impact | |||
|---|---|---|---|---|---|
| Loi | min | mode | max | ||
| r1 à r5 | 1 | Uniforme | 5 | 10 | |
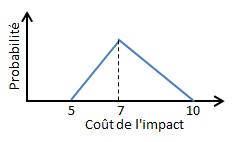
| r6 à r10 | 0,35 | Triangulaire | 5 | 7 | 10 |
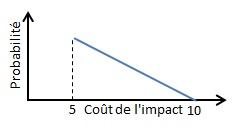
| r11 à r15 | 0,7 | Triangulaire | 5 | 5 | 10 |
| r1 à r5 | r6 à r10 | r11 à r15 |
|---|---|---|
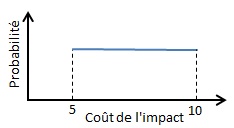 |  |  |
Le risque r2 a une probabilité d’occurrence égal à 1 et son impact est décrit par une loi Uniforme continue sur l’intervalle [5 ; 10]
Le risque r12 a une probabilité d’occurrence égal à 0,7 et son impact est décrit par une loi Triangulaire (5 ; 5 ; 10) car la valeur minimale est aussi la plus probable.
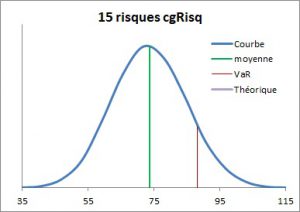
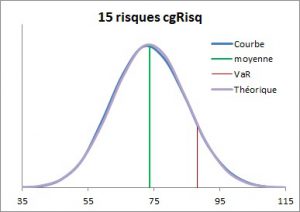
Le risque global, obtenu en faisant la somme des 15 risques élémentaires avec 50 000 itérations, est une variable aléatoire dont les caractéristiques sont présentées dans le cadre suivant .
Les sommes des min et des max peuvent facilement se vérifier à partir des données des 15 risques. Les autres résultats sont obtenus par la simulation. On peut noter que l’intervalle [min=33; max=116] de la somme est plus restreint que l’intervalle [somme des min=25; somme des max=150].
La VaR90 (valeur à risque à 90%) représente la borne supérieure de la somme qui a une probabilité de 10% d’être dépassée. Si l’on accepte cette couverture (= risque de 10% de se tromper), on peut considérer que le risque global est inférieur ou égal à 88,24. Cette valeur est bien inférieure à 150 et 116 ci-dessus. Si l’on veut modifier le risque de se tromper, et donc le montant de la VaR, on peut retenir une autre VAR (80, 85, 95, etc.).
La valeur retenue en fonction du taux de couverture, ici la VaR90, permet de définir la provision pour risque du projet, sachant qu’on lui associe une probabilité. Le coût prévisionnel d’un projet n’est jamais une valeur déterministe. La valeur affichée est nécessairement associée à une probabilité.
5 – Intérêt
L’analyse quantitative des risques apporte deux avantages d’égale importance : le résultat (estimation des provisions) et la mise en place de procédures permettant de l’obtenir. Ces deux aspects se retrouvent systématiquement dans toutes les approches quantitatives, insuffisamment mises en œuvre dans la gestion des grands projets dont les coûts dépassent souvent les prévisions initiales.
- L’analyse quantitative produit des estimations permettant de définir des provisions associées à des probabilités (VaR50, Var85, VaR95, etc.). La provision retenue résulte d’une analyse détaillée des multiples composantes du projet ce qui améliore sa qualité, sa visibilité et sa crédibilité.
- Pour obtenir un résultat fiable et crédible, il est nécessaire de procéder à un examen complet, détaillé, approfondi des risques du projet et d’adapter les pratiques, les méthodes et les outils (logiciels de calcul et bases de données) à cette approche collective. Ce travail bénéficie nécessairement à la qualité du projet dans son ensemble. Les pratiques mises en place pour obtenir le résultat sont au moins aussi importantes que le résultat lui-même.
L’analyse quantitative des risques permet de dimensionner la provision pour risque d’un projet de façon probabiliste, ce qui fournit un outil de gestion très utile aux responsables du projet.
L’analyse de risque n’est pas limitée au coût global. Elle peut porter sur toute estimation financière, coût global ou non.
6 – Application disponible en ligne
Une application permettant de faire la somme de risques est disponible dans l’onglet « Simulateur » qui apparait sous l’onglet « Agréger les risques ». On peut aussi l’atteindre en cliquant sur le lien suivant: Simulateur
Pour l’utiliser, il suffit de :
-
Lire la présentation et les explications;
-
Saisir des risques dans un tableau dont on peut adapter la dimension (bouton « Ajouter »);
-
Cliquer sur le bouton « Valider » pour vérifier qu’il n’y a pas d’erreurs de saisie et afficher un premier jeu de résultats;
-
Cliquer sur le bouton « Simulation » pour obtenir les résultats numériques et graphique.