pour calculer la somme de risques indépendants
L’application disponible dans cette page se situe dans le cadre de l’analyse quantitative des risques. C’est une version améliorée du simulateur de sommes de variables aléatoires indépendantes disponible dans l’onglet « Risques » du site coutglobal.fr. C’est aussi une version très simplifiée du logiciel evaRisq, actuellement utilisé pour estimer la provision pour risques de grands projets.
- Modélisation d’un risque: trois lois sont disponibles (Binaire, Uniforme, Triangulaire)
- Saisie des données
- Simulateur
- Complément
1 – Modélisation d’un risque
Définition : Un risque est un événement dont l’occurrence et/ou l’impact ne peuvent être prévus avec certitude. Il est donc modélisé par une probabilité d’occurrence et un impact.
La probabilité d’occurrence (Pocc) est représentée par une valeur unique (par exemple Pocc=1 si le risque est certain ou Pocc=0.6 si sa probabilité est de 60%).
L’impact du risque est évalué en termes de coût par les experts du domaine concerné qui ont participé à l’analyse de risque. L’unité monétaire (euro, dollar, livre…) n’est pas mentionnée ici. Cet impact n’étant pas une valeur certaine, il est modélisé par une variable aléatoire (VA) qui représente au mieux les conséquences possibles du risque (c’est à dire les coûts générés par la réalisation de l’évènement ) avec les probabilités associées.
Dans cette application disponible en ligne, trois lois sont actuellement retenues pour décrire un risque X.
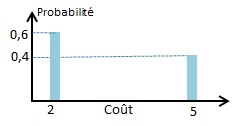
Loi Binaire
X peut prendre 2 valeurs : x1 avec la probabilité p et x2 avec la probabilité 1-p. A noter que si l’on considère la Pocc (X = 0 avec la probabilité 1-pocc), la variable X peut alors prendre 3 valeurs : 0, x1 et x2
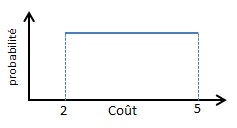
Loi Uniforme continue
X peut prendre toutes les valeurs comprises dans l’intervalle [Min; Max], et ces valeurs sont équiprobables
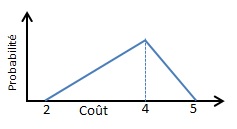
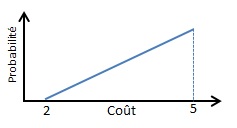
Loi Triangulaire
X est défini par les 3 valeurs [Min; Mode; Max], le Mode étant la valeur la plus probable. De plus, les probabilités associées à ces valeurs évoluent de façon linéaire pour représenter un triangle dont le sommet se situe au Mode.
2 – Saisie des données
La saisie des données est effectuée manuellement à l’aide du tableau ci-dessous, situé entre les 2 filets de séparation rouges. Ce tableau comporte une ligne qui contient deux risques, numérotés 1 et 2. Chaque risque contient 5 cases situées dans les colonnes Pocc ; Loi ; Min/x1 ; Mode/p ; Max/x2
Pocc : La probabilité d’occurrence (Pocc) est une valeur unique comprise entre 0 et 1. Si Pocc = 1 (valeur par défaut), le risque se réalise sûrement. Sinon sa probabilité, qui est > 0, est < 1 (0.4 ou 0.7 etc.) . Si la case reste vide (pour simplifier et accélérer la saisie) ou égale à 0, Pocc est égale à 1 par défaut. Un risque dont la probabilité d’occurrence est nulle n’existe pas.
Impact Remplir les cases en appliquant les règles suivantes:
| Loi | Min/x1 | Mode/p | Max/x2 |
|---|---|---|---|
| u ou vide pour Uniforme t pour Triangulaire b pour Binaire | Valeur min pour Uniforme et Triangulaire Valeur x1 pour Binaire | Vide pour Uniforme Mode pour Triangulaire Probabilité p pour Binaire | Valeur max pour Uniforme et Triangulaire Valeur x2 pour Binaire |
Conseils pour le premier essai
- Conserver les 2 risques (vides) du tableau sans en ajouter de nouveaux;
- Laisser les cases des colonnes Pocc vides. Par défaut la probabilité d’occurrence est égale à 1 (risque certain);
- Laisser les colonnes Loi vides. Par défaut la loi Uniforme est retenue;
- Saisir 0 (zéro) dans les colonnes Min/x1 et 5 dans les colonnes Max/x2. Vous avez saisi 2 risques Uniforme continus dans l’intervalle [0; 5];
- Cliquer sur Valider. Des résultats que vous pouvez vérifier facilement s’affichent;
- Cliquer sur Simulation. Les résultats apparaissent dans un nouvel onglet. Constater que la somme de 2 lois Uniforme est une loi Triangulaire. A noter que dans cette application, la distribution de probabilité du résultat est représentée par une courbe continue, obtenue en lissant les points de l’histogramme;
- Revenir dans le tableau et cliquer sur le bouton Ajouter. Saisir les mêmes paramètres pour les 2 nouveaux risques qui s’affichent. Cliquer sur Valider puis sur Simulation. La somme commence à ressembler à une courbe en cloche. Vous pouvez continuer avec des risques différents.
Rappels et remarques
- Le nom de la loi (u pour Uniforme, t pour Triangulaire et b pour binaire) est en minuscule. Si la case est vide, u est sélectionnée par défaut;
- Si la loi est Triangulaire (t) il faut saisir un mode (valeur la plus probable) compris entre le Min et le Max;
- Si Pocc est vide, la probabilité d’occurrence est égale à 1 par défaut;
- les probabilités sont toujours comprises entre 0 et 1;
- Les décimales s’écrivent avec un point et non une virgule;
- Cliquer sur le bouton « Ajouter » autant de fois qu’il est nécessaire pour saisir la liste des risques. Vous pouvez ajouter des lignes au fur et à mesure ou bien afficher toutes les lignes avant de commencer la saisie des données. Les lignes affichées ne peuvent plus être supprimées, cependant s’il y en a trop les dernières peuvent rester vides, elles ne seront pas prises en compte;
- En cliquant sur le bouton Valider, des résultats calculés avant la simulation sont affichés s’il n’y a pas d’erreurs dans la saisie. Attention, ce n’est pas une zone de saisie.
A noter que selon le navigateur utilisé, les axes de la représentation graphique (abscisse = coût et ordonnée » probabilité) peuvent ne pas apparaître. Ce problème sera corrigé prochainement.
3 – Simulateur
4 – Compléments
Les données sont saisies manuellement par l’intermédiaire du tableau, ce qui peut être laborieux avec une liste de 50 risques ou plus, surtout si l’opération est renouvelée le lendemain après en avoir modifié 5. Il est donc envisageable de pouvoir sauvegarder la liste sur fichier pour la ré-exploiter ultérieurement.
La somme des risques est une variable aléatoire (VA) décrite par une distribution de probabilité. Les résultats affichés sont détaillés dans la page « Agréger les risques ». A noter que cette distribution est représentée par une courbe continue. Elle est donc peu significative si la liste ne comporte que quelques risques binaires(b). Le théorème central-limite nous apprend que la somme de variables aléatoires indépendantes converge en loi vers une loi Normale (Laplace-Gauss) dont le graphique ressemble à une courbe en cloche. Le résultat obtenu peut cependant être différent d’une cloche si le nombre de risques est faible et si les pocc sont différentes de 1.
La VaR (Valeur à Risque) est un quantile de la variable aléatoire « Somme des risques », ce quantile étant associé à un pourcentage ou une probabilité. Par exemple la VaR90 est égale à la borne supérieure de la VA Risque-Global qui n’est dépassée que dans 10% des cas. En retenant la VAR90 comme valeur de la provision pour risques, on est assuré de couvrir les risques du projet avec une probabilité de 0.9 de ne pas la dépasser. Il est bien sûr possible de retenir une autre valeur pour la provision (VaR80, VaR85, VaR95, etc.) en fonction du risque de la dépasser que l’on accepte de prendre. Dans cette application, c’est la VaR90 qui est estimée.
Des contrôles sont effectués lors de la lecture des données et certaines erreurs de saisie sont corrigées sans que cela apparaisse dans le tableau. Par exemple si Pmin=1 la valeur de Pmax est ignorée. Cette première version en ligne peut cependant comporter des oublis concernant les contrôles de saisie. Vous pouvez donc me contacter ou laisser un commentaire pour me faire part de problèmes éventuels ou pour faire des remarques sur cette application.