» De manière générale, au-delà des discours sur le principe de précaution, la prise en compte effective des risques dans les études et les évaluations qui aliment la décision reste insuffisante au regard des enjeux. L’absence de réflexion sérieuse sur ce point inflige à posteriori à la collectivité des coûts supplémentaires importants qui auraient pu être évités. » Rapports et documents 2011 n°36 – Centre d’analyse stratégique.
- Prise en compte de l’aléa : Risques projet / Risques d’incertitude
- Management des risques
- Analyse quantitative : Mise en œuvre / Modélisation des risques
- Quelques lois de probabilité
- Agrégation des risques : Coût d’un projet
1 – Prise en compte de l’aléa
Il n’est ni sérieux ni réaliste d’estimer le coût prévisionnel d’un projet complexe, pouvant s’étaler sur une longue période, avec une modélisation déterministe. Les dépenses réelles constatées dans le déroulement du projet seront nécessairement différentes des prévisions faites lors de la préparation du projet. Cet écart entre la prévision et la réalisation a principalement deux causes :
- Le projet ne s’est pas déroulé conformément au scénario initial qui a été perturbé par des évènements non prévus;
- Les données élémentaires prévisionnelles utilisées pour estimer les coûts associés au scénario se sont avérées inexactes .
La notion de risque n’est pas limitée à des événements redoutés et peut s’étendre à des événements souhaités que l’on nomme généralement « opportunité ». C’est le cas de situations telles que gagner au jeu, réussir un examen ou payer un produit moins cher que prévu.
1.1 – Risques projet
Les risques projet incluent ici les risques techniques, réglementaires, contractuel, financiers, etc. Ils permettent de prendre en compte les événements non prévus mais prévisibles, susceptibles d’impacter négativement ou positivement le déroulement de chaque scénario.
Dans chaque situation, la liste des risques à considérer dépend de la nature du projet et du scénario qui le décrit. Pendant la phase d’identification des risques, il est utile de s’appuyer sur une liste générique qui contient par exemple les risques suivants.
| • Pollution : Le stockage, la manipulation et le transport de certaines matières nécessitent des précautions particulières qui n'excluent cependant pas la possibilité d'accidents. • Problèmes de construction liés à l'état du sol et du sous-sol : Lorsque le projet démarre par des travaux de terrassement, ceux-ci peuvent être entravés par l'état du sol ou du sous-sol. • Disponibilité : Ce risque apparaît lorsque la mise à disposition des installations et des matériels ne répond pas aux exigences de disponibilité contractuelles. • Évolution des besoins : les évolutions des besoins du client peuvent avoir ou non un impact sur la nature ou le dimensionnement des constructions et équipements à mettre en place puis à soutenir pendant la durée du projet. | • Délais de conception et réalisation : toute variation des délais a pour effet de déformer le scénario de base et donc d'impacter le coût global du projet. • Non atteinte des performances contractuelles • Modifications législatives, réglementaires ou normatives spécifiques ou non au secteur concerné : évolution du droit social (Salaire minimum, durée du temps de travail, charges patronales, retraite, etc.), des normes antipollutions (bruit, émission de gaz…) et de sécurité (conditions de travail, transport de produits à risques…). • Variation des coûts d'assurances |
1.2 – Données incertaines ou risques d’incertitude
Incertitude = connaissance imparfaite dans différents types de situations
Le coût d’un projet est estimé à partir de données prévisionnelles qui couvrent entre autres les aspects suivants:
- Données économiques et financières telles que taux d’inflation, taux d’intérêt, taxes, OAT, …;
- Coûts ou prix unitaires d’études, de conception, de construction des ouvrages, de production (ou d’acquisition) ou de location de matériels et équipements, coût des services et de la main d’œuvre, etc.;
- Dimensionnement des infrastructure et des installations, des moyens matériels et humains, …
L’incertitude peut avoir deux causes
- Selon la phase de l’étude préalable et donc la maturité du projet, certains choix de conception ou de construction ne sont pas encore définitivement arrêtés. Il peut en être de même pour les scénarios d’utilisation (exploitation et maintenance) pendant la phase de construction ou d’acquisition. La connaissance imparfaite des travaux à réaliser génère automatiquement une imprécision sur leurs coûts.
- Lorsque le projet est bien déterminé, il reste une incertitude sur les prix du marché ou les possibilités de négociation.
Ces incertitudes sont assimilées à des risques car elles ont un impact identique et subissent le même traitement mathématique. On les nomme ici « risques d’incertitude ».
2 – Management des risques
Tout projet est soumis à des aléas susceptibles de mettre en cause la tenue de ses objectifs définis en termes de coûts, délais et performances. Ces aléas concernent aussi bien le déroulement des différentes phases du projet (risques projet) que le fonctionnement des systèmes mis en œuvre et les accidents éventuels qu’ils peuvent occasionner (risques système). Ils sont ici regroupés sous l’appellation « Risques projet ».
Le management des risques est une démarche d’anticipation des évènements redoutés dans le déroulement d’un projet. Il consiste à :
- identifier les événements redoutés susceptibles de mettre en cause les objectifs du projet;
- estimer la criticité des risques en termes de probabilité d’occurrence et de gravité des conséquences;
- mettre en place les actions de maîtrise des risques du projet à partir de la liste des risques triés par ordre de criticité décroissante;
- suivre les risques en relation avec les actions mises en place et capitaliser le retour d’expérience.
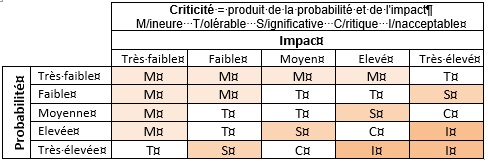
La criticité des risques est représentée ci-dessous de façon synthétique dans une matrice qui croise la probabilité d’occurrence et l’impact. Ce sont 2 variables aléatoires qualitatives définies par des modalités qui vont de « Très faible » à « Très élevé ».
3 – Analyse quantitative
L’analyse quantitative est la deuxième étape à réaliser après l’analyse qualitative. Elle a pour finalité d’estimer l’impact financier des risques de toute nature et de l’intégrer dans le coût du projet, en particulier pour estimer la provision pour risques. La part du coût associée aux risques n’est alors pas calculée à partir de coefficients forfaitaires de provisions et de marges mais résulte d’une analyse rigoureuse et détaillée des risques portés par le projet (Voir §4). Cela offre une bonne visibilité en phase de négociation ou lors de la fixation d’un prix.
3.1 – Mise en œuvre
L’analyse de risque se déroule sur plusieurs phases :
- l’identification qui permet de dresser une liste exhaustive des risques à considérer dans l’étude (à partir d’une typologie générique des risques préétablie);
- l’analyse qualitative qui comporte la description de chaque risque, l’analyse des causes et des impacts, l’estimation qualitative de la probabilité d’occurrence et de l’impact (Cf. §3.2), le partage des risques entre les acteurs lorsque le projet en comporte plusieurs;
- la modélisation qui permet de traduire de façon quantitative les résultats de l’analyse qualitative;
- l’agrégation de l’ensemble des risques.
Les phases 1) et 2), réalisées dans le cadre du management des risques, concernent essentiellement les risques projet, les incertitudes étant naturellement définies lors de la valorisation des données.
3.2 – Modélisation des risques
Un risque est un événement dont l’occurrence et/ou l’impact ne peuvent être prévus avec certitude. Il est donc modélisé par une probabilité d’occurrence et un Impact. La modélisation se déroule sur trois phases.
3.2.1 – Définition du risque
La probabilité d’occurrence (pocc) d’un risque dépend principalement des causes de l’évènement redouté alors que l’évaluation de l’impact repose sur l’analyse des conséquences. Cependant, la cause et la conséquence, qui ne sont pas indépendantes, sont deux facettes du risque qu’il faut considérer simultanément.
A partir de quel délai un train ou un avion sont en retard. A partir de quelle amplitude un incident est-il un accident. Un retard de 2 mn est beaucoup plus fréquent qu’un retard de 2 heures. La probabilité d’occurrence est donc plus élevée dans le premier cas que dans le deuxième. En revanche le coût de l’impact est à priori plus faible. A la limite, il peut être décidé que le retard compte à partir de la première minute avec un coût presque nul. La pocc est alors égale à 1 et l’impact commence à 0. Ce cas est relativement fréquent.
La première étape de la modélisation d’un risque est sa définition, qui doit-être la plus précise possible et ne doit pas laisser place à l’ambiguïté. Elle doit être argumentée en explicitant les causes et les conséquences qui lui sont attachées.
3.2.2 – Plage des valeurs de l’impact
La phase suivante consiste à définir trois valeurs pour l’impact :
- la valeur minimale (Min);
- la plus probable (le Mode);
- la valeur maximale (Max).
Le Mode n’est pas nécessairement le centre de la plage et peut être plus proche du Min ou du Max, voire égal à l’un d’eux. En définissant l’intervalle [Min; Max], il est souhaitable de considérer en même temps le comportement du risque au voisinage des bornes.
Si les bornes Min et Max sont certaines, toute valeur extérieure à l’intervalle [Min ; Max] a une probabilité nulle: le risque est borné. Dans le cas contraire, les bornes non certaines sont associées à une probabilité. Par exemple, le retard maximum est fixé à 5 heures avec une probabilité de 0,95. Le risque est non borné car le maximum pourrait être dépassé dans 5% des cas, évènement rare mais pas impossible.
Cette étape est importante mais délicate car il n’est pas facile de déterminer ces valeurs. Pour éviter les erreurs, il est nécessaire que ces choix soient argumentés avec des éléments tangibles, des considérations techniques ou l’analogie avec des situations similaires. Ces arguments doivent être enregistrées pour revenir éventuellement sur l’analyse du risque.
3.2.3 – Modélisation du risque
Probabilité d’occurrence
La probabilité d’occurrence est généralement représentée par une valeur unique ou bien une loi de probabilité simple sur [0; 1] ou sur un intervalle inclus dans [0; 1].
Pour les risques d’incertitude, la probabilité d’occurrence est égale à 1 sinon l’incertitude n’existerait pas.
Modélisation de l’impact
L’impact est modélisé par une variable aléatoire qui associe une probabilité à chaque valeur de la plage [Min; Max] retenue (*). L’impact peut être modélisé par une loi (ou distribution) de probabilité paramétrique,
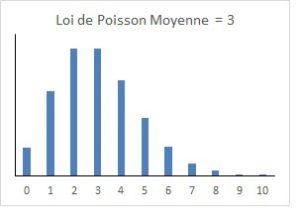
- Discrète : Binaire, Binomiale, Poisson, Géométrique…
- Continue : Uniforme, Triangulaire, Normale, Log Normale, Exponentielle, Bêta…
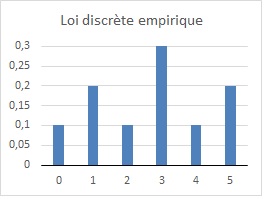
ou empirique, c’est-à-dire définies par les valeurs possibles et les probabilités associées.
(*) Une variable aléatoire est discrète si l’ensemble des valeurs qu’elle peut prendre est fini ou infini dénombrable. Dans le cas contraire, elle est continue. Si la variable est continue, la probabilité de chaque point de l’intervalle [Min; Max] est nulle. La probabilité d’une valeur est remplacée par la densité de probabilité qui représente la probabilité d’un très petit intervalle qui encadre la valeur.
Pour modéliser un risque, l’expert se base, par ordre décroissant, sur :
- la connaissance d’éléments objectifs issus de l’analyse des causes et des conséquences possibles;
- l’analogie avec des situations similaires;
- une intime conviction justifiée par l’expérience.
Valorisation des impacts : Les impacts sont généralement définis en termes de coûts, délais ou performances. Si l’analyse de risques s’insère dans l’estimation du coût d’un projet, il peut être utile, voire nécessaire, de traduire les impacts « délais » ou « performances » en termes de coûts.
4 – Quelques lois de probabilité
Il existe de nombreuses lois de probabilité, discrètes ou continues, pouvant être utilisées pour modéliser un risque (un impact). Ces lois permettent de représenter les situations suivantes.
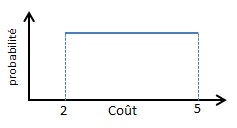
- Toutes les valeurs sont équiprobables, c’est-à-dire ont la même probabilité. Il n’y a pas de Mode. Le lancer d’un dé non truqué est un exemple simple d’une variable discrète Uniforme ;
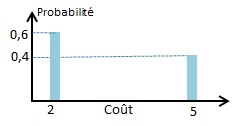
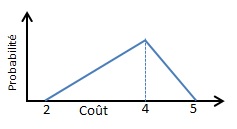
- Les valeurs ne sont pas équiprobables, et la variables est bornée. Les valeurs extérieures à [Min; Max] ont des probabilités nulles;
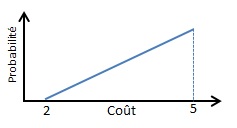
- Les valeurs ne sont pas équiprobables, et la variables est non bornée. La valeur d’une borne est alors associée à une probabilité. Par exemple, le retard maximum est fixé à 5 heures avec une probabilité de 0,95.
Quelques exemples sont présentés ci-dessous.
| Cas 2 - Variable discrète : loi Binaire | Cas 2 - Variable discrète empirique | Cas 3 - Variable discrète paramétrique loi de Poisson |
|---|---|---|
| X peut prendre deux valeurs : x1=2 avec la probabilité p=0.6 et x2=5 avec la probabilité 1-p=0.4 | Généralisation de la loi Binaire à plus de 2 valeurs. X peut prendre 6 valeurs dont les probabilités sont indiquées en ordonnées. Leur somme vaut 1 | X = nombre d'événements de probabilité donnée se produisant dans un intervalle de temps donné. Cette variable n'est pas bornée. Par exemple la probabilité de la valeur 20 n'est pas nulle P(X = 20) = 7,14 E-11 |
 |  |  |
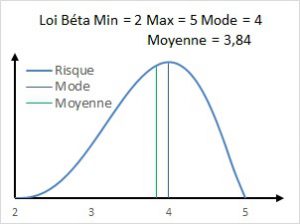
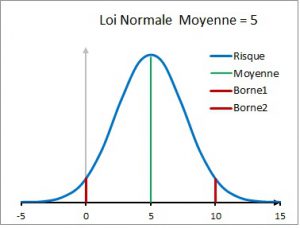
La variable continue X est bornée dans l’intervalle [2; 5]
| Cas 1 : loi Uniforme | Cas 2 : loi Triangulaire | Cas 2 : loi Triangulaire | Cas 2 : loi Bêta |
|---|---|---|---|
| X peut prendre toutes les valeurs comprises dans l'intervalle [2; 5]. Elles sont équiprobables | Le Mode est égal à 4 et la probabilité des valeurs évolue de façon linéaire entre le Mode et les bornes | Le Mode est égal à 5. Si Mode = 2, la figure est inversée. | Le Mode est égal à 4 et la probabilité des valeurs n'évolue pas de façon linéaire entre le Mode et les bornes (différent de Triangulaire) |
 |  |  |  |
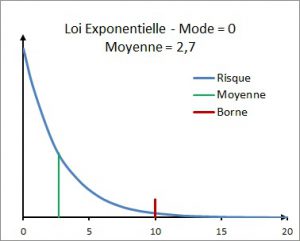
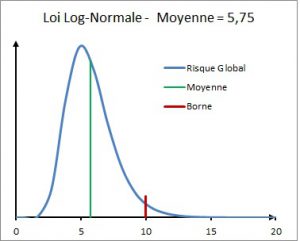
La variable continue X est définie dans l’intervalle [Min=0; Max=10]. Elle n’est pas bornée. Les bornes sont donc estimées avec une probabilité de 0,025 c’est-à-dire que chaque borne (Min ou Max) pourrait être dépassée dans 2,5% des cas. Les résultats des exemples sont obtenus avec une simulation de Monte-Carlo sur 100 000 itérations.
| Cas 3 : loi Exponentielle | Cas 3 : loi Normale | Cas 3 : loi Log-Normale |
|---|---|---|
| Mode = Min = 0 ; Moyenne = 2,7 La variable est bornée à gauche mais pas à droite. Sa valeur décroit rapidement vers 10. La valeur la plus grande obtenue au cours de la simulation est égale à 41. A noter que la moyenne tombe à 2,46 si l'on rejette toutes les valeurs supérieures à 10 | La loi Normale est symétrique Mode = Moyenne = 5 95% des valeurs sont dans l'intervalle [0; 10], 2,5% sont à gauche et autant à droite. Lors de la simulation du risque, l'utilisateur a le choix de retenir ou non les valeurs extérieures à l'intervalle. | Min = 0 ; Mode = 5 ; Moyenne = 5,75 La variable est bornée à gauche mais pas à droite. 2,5% des valeurs sont supérieures à 10. La valeur la plus grande obtenue au cours de la simulation est égale à 25. A noter que la moyenne tombe à 5,61 si l'on rejette toutes les valeurs supérieures à 10 |
 |  |  |
5 – Agrégation des risques : coût d’un projet
Le coût du projet est égal à la somme :
- des rubriques de coûts définies par la structure de coûts du projet
- des risques projet identifiés lors de l’analyse de risques
Les rubriques de coûts calculées à partir de données entachées d’incertitude ainsi que les risques projet sont des variables aléatoires. Il en est donc de même du coût du projet qui n’est autre qu’une somme de variables aléatoires et de valeurs constantes (les rubriques calculées avec des données certaines).
Un exemple sur la « Prise en compte de l’aléa dans l’analyse du Coût Global » à consulter à l’adresse Comparaison de plusieurs scénarios
Pour la mise en œuvre de l’agrégation des risques, voir Risque Global