AMDEC
L’Analyse des Modes de Défaillance, de leurs Effets et de leur Criticité est un outil de Sûreté de Fonctionnement. C’est une démarche qui consiste à identifier au niveau d’un système ou d’un de ses sous-ensembles, les modes potentiels de défaillance de ses éléments, leurs causes et leurs effets. Elle a entre autres pour objet de déterminer les points faibles du système et d’y apporter des remèdes en conception.
ASL
L’analyse du soutien logistique a pour objectif :
- d’optimiser les caractéristiques du système et de son soutien;
- pour répondre aux exigences de coût global / disponibilité;
- par l’étude d’alternatives et le choix des meilleurs compromis.
Ces études, qui sont répétées de façon itérative pendant la conception/réalisation, couvrent les domaines suivants : Analyse fonctionnelle, sûreté de fonctionnement (fiabilité, maintenabilité, disponibilité, sécurité), analyse des tâches de maintenance, analyse des niveaux de réparation, modularité, testabilité, AMDEC.
L’ensemble des données produites par ces analyses est regroupé dans une base de données logistique.
Coûts directs et indirects
Les coûts directs peuvent être facilement affectés (sans ambiguïté et sans analyse intermédiaire) à un système car ils ne se rapportent qu’à ce système.
Les coûts indirects se rapportent à plusieurs systèmes et doivent faire l’objet d’une répartition (à l’aide d’une clé) avant d’être imputés à chacun des systèmes. Les coûts indirects (et donc imputables à plusieurs systèmes) ne se comportent pas de la même manière avec l’introduction d’un nouveau système. Certains coûts indirects peuvent varier tandis que d’autres restent sans changement. Les notions « fixe » et « variable » sont alors définies relativement à la situation précédant l’introduction du nouveau système.
Densité de probabilité
Une VA discrète notée X est définie par un ensemble de couples (xi / pi) où les xi désignent les valeurs de X est les pi les probabilités associées. Il est indispensable que la somme des pi soit égale à 1.
Lorsque la VA est continue, le nombre de valeurs possibles étant infini, il n’est pas possible d’associer une probabilité à chaque valeur. Dans ce cas, on définit la probabilité associée à chaque petit intervalle de l’ensemble des valeurs possibles. Pour cela, on associe à chaque valeur x de X un intervalle [x ; x+dx], avec dx très petit, auquel on associe une probabilité f(x) dx.
f(x) dx = Proba(x < X < x+dx). La fonction « f » est la densité de probabilité de la variable X.
Ecart type
Les variables aléatoires sont généralement caractérisées par plusieurs paramètres dont les plus importants sont la moyenne (caractéristique de tendance centrale) et l’écart type (caractéristique de dispersion). L’écart type est une mesure de l’écart entre la moyenne et les valeurs de la variable.
Pour une moyenne donnée, la dispersion des valeurs possibles autour de la moyenne est d’autant plus grande que l’écart type est élevé. Lorsque l’écart type est petit, les valeurs possibles sont proches de la moyenne. Le risque d’obtenir une valeur très éloignée de la moyenne est alors faible.
Éléments de soutien
Un système est généralement décomposé en deux ensembles de produits : le système principal qui assure la ou les fonctions attendue(s) (par exemple avion, camion, radar…) et les éléments de soutien qui regroupent l’ensemble des moyens logistiques à mettre en place (ou à adapter à partir d’éléments existants), spécifiques au système, pour la durée de vie du système. Il s’agit par exemple des données techniques et de la documentation, des rechanges, des équipements de test et de soutien, des moyens de formation, des infrastructures…
Un objectif majeur du soutien logistique intégré (SLI) est d’assurer la cohérence entre le système principal et les éléments de soutien lors de la conception du système afin d’obtenir la disponibilité souhaitée au moindre coût global (qui rappelons le, inclut l’acquisition, l’exploitation et le soutien du système principal et des éléments de soutien).
Cependant, et par abus de langage, le terme système est souvent utilisé pour désigner le système principal (peut-être même dans ce site).
Modélisation
Un modèle est une représentation simplifiée d’un système réel, conçue et utilisée pour évaluer et prévoir certains comportements de ce système. Il ne s’agit pas d’une représentation unique de la réalité; ainsi la modélisation d’un avion est différente selon que l’on souhaite étudier ses caractéristiques aérodynamiques, ses performances opérationnelles, sa fiabilité, ses coûts, etc. Seuls les modèles abstraits sont concernés ici, à l’exclusion de toute reproduction matérielle telles que maquettes ou modèles réduits.
Ici, un modèle est une représentation mathématique ou algorithmique simplifiée mais suffisamment fidèle du projet pour fournir des estimations prévisionnelles crédibles du coût global.
Un modèle peut être déterministe ou stochastique. Dans le deuxième cas, le comportement aléatoire du système est représenté par des lois de probabilité.
Un modèle contient généralement d’autres modèles. C’est le cas pour la modélisation du coût d’un projet lorsque les risques sont eux-mêmes modélisés par des variables aléatoires.
Lorsque le système étudié est connu, le modèle permet de prévoir le comportement du système en réponse à une entrée (utilisation déductive du modèle). Dans le cas contraire (utilisation inductive), le modèle permet de définir certaines caractéristiques du système afin d’obtenir un comportement ou un résultat souhaité. Le modèle est alors utilisé comme outil d’aide à la conception du système.
Quelques Techniques de base utiles en modélisation
Mathématiques, probabilités et statistiques, simulation, simulation de Monte-Carlo, estimation des coûts, analyse des risques, modélisation économique et financière, FMD (fiabilité, maintenabilité, disponibilité), gestion et dimensionnement des stocks de rechanges.
SLI
Le soutien logistique intégré est défini comme une approche coordonnée, unifiée et itérative de la gestion et des activités techniques nécessaires à :
- Intégrer la prise en compte du soutien dans la conception des systèmes et équipements (en particulier à travers ses spécifications opérationnelles et techniques), en accord avec les objectifs de disponibilité et de coût;
- Développer les éléments du soutien;
- Acquérir et fournir le support requis durant toute la vie opérationnelle.
Le SLI a pour objectifs :
- La recherche d’un haut niveau de fiabilité et de disponibilité opérationnelle;
- La réduction du coût global.
Soutien logistique
Le soutien logistique regroupe l’ensemble des procédures et prestations destinées à assurer la disponibilité d’un système pendant sa durée de vie, en tenant compte des conditions d’utilisation. Ces procédures et prestations sont regroupées en six grandes fonctions :
- Management
- Maintenance
- Réapprovisionnement
- Conditionnement, emballage, manutention, stockage et transport (CEMST)
- Formation continue
- Maintien de l’aptitude au soutien
Système
Le terme système, utilisé ici de façon générique, peut être définit comme un ensemble d’éléments (sous systèmes ou composants) qui fonctionnent de façon coordonnée afin de concourir à un résultat. L’analyse du coût global peut être limitée à un sous système.
Exemples de systèmes : un équipement, un matériel terrestre, aérien ou naval, un ouvrage, un bâtiment, un ensemble fonctionnel tel qu’un hôpital, une installation sportive, une prison, un parc d’éoliennes, un aéroport, un parc de loisirs.
Taux de rentabilité interne (TRI)
Un investissement peut être couvert par de la dette et des fonds propres.
Soit l’échéancier constitué d’une parts des fonds propres apportés et d’autres part des dividendes distribués pour rémunérer ces fonds propres. Le taux de rentabilité interne de l’investissement est égal à la valeur du taux d’actualisation qui annule la VAN de cet échéancier.
C’est le taux d’intérêt pour lequel la valeur actuelle des dividendes est égale à la valeur actuelle des fonds propres.
Valeur actuelle et actualisation
L’introduction d’un taux d’actualisation (de dépréciation, de déflation) procède du principe qu’un euro aujourd’hui a plus de valeur qu’un euro dans un an. Les montants annuels d’un échéancier de dépenses, même s’ils sont identiques, n’ont donc pas la même valeur actuelle pour le décideur.
Si « a » est le taux d’actualisation (les Anglo-saxons utilisent le terme « discount rate »), la valeur actuelle d’un euro dans 1 an est égale à 1/(1+a) (donc inférieure à 1, « a » étant compris entre 0 et 1). Il s’ensuit que la valeur actuelle d’un euro dans n années est égale à 1/(1+a)n si les taux d’actualisation sont constants.
1/(1+a)k est le coefficient d’actualisation de la k-ème année.
Pour transformer un échéancier en euros actualisés, il suffit de multiplier le montant de chaque année par le coefficient d’actualisation de l’année. La somme des montants de l’échéancier est alors égale à la valeur actuelle du projet, souvent désigné par VAN (valeur Actuelle Nette).
Si Fi est un échéancier de dépenses et de recettes sur n+1 années (l’année en cours est l’année 0), la VAN de l’échéancier est égale à :
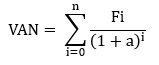
Valeur résiduelle
Lorsque l’étude porte sur un projet dont la durée est inférieure à la durée de vie du bien, les coûts de retrait de service sont remplacés par la valeur résiduelle en fin de projet.
Cette valeur provient généralement d’une estimation théorique basée sur une hypothèse de dégressivité (linéaire ou non) de la valeur en fonction de l’âge. Cette hypothèse peut être mise en défaut par exemple si le bien prend de la valeur avec l’âge ou si les progrès technologiques le rendent obsolète. C’est pourquoi il est conseillé d’accompagner cette estimation d’un « risque de valeur résiduelle » à modéliser au cas par cas en fonction de la nature du système et du contexte prévisible à l’échéance du projet.
La valeur résiduelle est systématiquement prise en compte (en euros actualisés) pour comparer plusieurs options (analyse économique). Lorsque le coût global est utilisé pour prévoir les échéanciers de dépenses et de recettes (analyse financière), sa prise en compte dépend du scénario.
Valeur à risque (VaR)
La valeur à risque (en statistique, centile ou quantile) d’une variable aléatoire représente la valeur maximale associée à une probabilité donnée (ou à un risque donné). Par exemple le quantile à 90% (VaR90) est égal à la valeur de la variable qui n’est dépassée que dans 10% des cas. Autre formulation: 90% des valeurs de la variable sont inférieures à VaR90.
Si l’on accepte cette couverture (= risque de 10% de se tromper), on peut considérer que le risque global est inférieur ou égal à VaR90. Si l’on veut modifier le risque de se tromper, et donc le montant de la VaR, on peut retenir une autre VAR (80, 85, 95, etc.).
Variable aléatoire
Une variable déterministe (ou certaine) est définie par une valeur unique. Par exemple, la taille de Jean est égale à 1,72 mètres.
Si l’on considère la taille d’un élève tiré au hasard dans la classe de Jean, on constate qu’elle est comprise entre 1,61m pour le plus petit et 1,85 pour le plus grand. La taille d’un élève de la classe de Jean est alors une variable aléatoire (VA) définie pour l’instant par ses valeurs minimale et maximale. A cette variable aléatoire, on peut associer une valeur moyenne obtenue en faisant la moyenne des tailles de la classe.
Une variable aléatoire peut être qualitative ou quantitative.
Dans le premier cas, les valeurs possibles sont définies par des modalités non mesurables, par exemple les partis politiques (LR, LREM, RN, MODEM, PC, etc.), les couleurs (Bleu, blanc, rouge, etc.), les appréciations attribuées par les professeurs de Jean (A, B, C, D, E). Si les 2 premières sont dites nominales, la 3ème est ordinale car elle permet de définir un ordre sur les élèves notés.
Les variables quantitatives sont définies par des valeurs numériques. Elles peuvent être discrètes (un nombre fini de valeurs) ou continues (intervalle de valeurs dans l’ensemble des réels). Le résultat d’un lancer de dés est une VA discrète qui prend les valeurs de 1 à 6. La taille des élève de la classe de Jean est une VA continue, bien que la notion de continue soit limitée ici par la précision de l’instrument de mesure qui procède à des arrondis au cm près.
Une variable aléatoire est décrite par une distribution de probabilité qui définit l’ensemble de ses valeurs (qualitatives ou quantitatives) et les probabilités associées. Les valeurs possibles pour un lancer de dès sont définis par l’ensemble {1, 2, 3, 4, 5, 6}, la probabilité de chacune des valeurs étant égale à 1/6 si le dés n’est pas truqué. A la veille d’élections, les organismes de sondage diffusent les probabilités de vote pour chacun des partis.
Les VA sont décrites par des distributions (ou lois) paramétriques discrètes (Bernouilli, Binomiale, Hypergéométriques, Poisson…) ou continues (Normale, exponentielle, LogNormale, Gamma…). Elles peuvent aussi être décrites par des lois empiriques définies par l’utilisateur.
Variable aléatoire Uniforme
Une variable est définie par une loi Uniforme si toutes ses valeurs ont la même probabilité.
